Python으로 라이브러리 사용 없이 3가지 테일러 급수 구현해보기

오늘은 Python으로 라이브러리 사용 없이 테일러 급수를 구현해보겠습니다

 

---

오늘 제가 구현할 테일러 급수는 아래의 3가지 함수입니다

첫 번째와 두 번째 함수는 정의역을 크게 고려하지 않고 코드를 짜도 무리는 없지만

 

세 번째 함수는 반드시 정의역을 만족시켜서 해야합니다

 

ln(x)로도 함수를 만들 수 있습니다

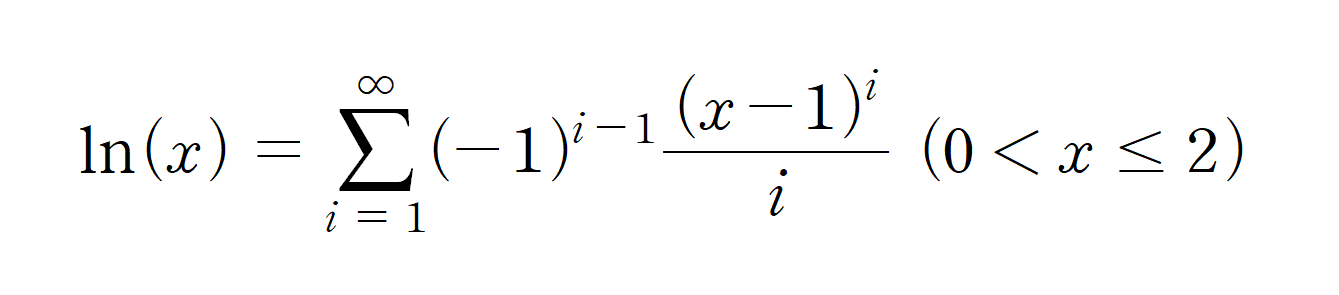
x 자리에 x-1을 대입하여 식을 다시 만들면 가능합니다 

 

정의역 역시 0<x≤2 로 바뀌게 됩니다

---

위에 조건들을 고려해서 짠 코드입니다

class lns:
  def __init__(self, v, n):
    self.v = v - 1
    if self.v < -1 or self.v > 1:
      print("Range out Value")

    global re
    self.re = []
    for i in range(1, n+1, 1):
      if i%2 == 0:
        self.a = -1 * ((self.v**i)/i)
        self.re.append(self.a)
      elif i%2 == 1:
        self.a = (self.v**i)/i
        self.re.append(self.a)
    self.result = sum(self.re)
    print(self.result)
#----------------------------------------------------------------------
class ex:
  def __init__(self, v, n):
    self.v = v
    global re
    self.re = []

    ss = [1]
    res = 1
    for k in range(1, n+1, 1):
      res *= k
      ss.append(res)
    print(ss)

    for j in range(0, n+1, 1):
      a = (self.v**j)/ss[j]
      self.re.append(a)
    self.result = sum(self.re)
    print(self.result)
#----------------------------------------------------------------------
class sinx:
  def __init__(self, v, n):
    self.v = v
    global re
    self.re = []

    ss = []
    for j in range(1, 2*n+2, 2):
      res = 1
      for k in range(1, j+1, 1):
        res *= k
      ss.append(res)

    for i in range(0, n+1, 1):
      if i%2 == 1:
        self.a = -1 * (self.v**(2*i + 1))/ss[i]
        self.re.append(self.a)
      elif i%2 == 0:
        self.a = (self.v**(2*i + 1))/ss[i]
        self.re.append(self.a)
    self.result = sum(self.re)
    print(self.result)

 

모든 class가 받는 인자는 x의 값과 몇 번째 항까지 근사를 할 건지입니다

 

가장 위에 lns의 경우 lns(1.1, 3)이면 ln(1.1)을 테일러 급수의 3번째 항까지 근사 시키라는 의미입니다

 

여기서 중요한 것은 결과값이 정확한 계산값이 아닌 근사값이라는 점 입니다

 

반드시 오차가 존재하고 이 오차를 확인해보겠습니다

 

3가지 함수를 비슷한 조건에서 비교하기 위해 모두 3번째 항까지 근사를 시켰습니다

---

① ln(1.1)

먼저 제가 만든 class의 근사값은 0.09533 정도로 나옵니다

공학용 계산기의 결과값과 비교하면 오차는 -2.3153533333417076e-05 로 매우 작았습니다

 

② sinx

제가 만든  class의 근사값은 0.09107정도가 나왔습니다

 

공학용 계산기의 sin값은 라디안을 취한 결과로 나옵니다

 

근사값과 비교해보면 오차는 -0.03873547233142847 정도가 나옵니다

 

③ e^3

제가 만든 class의 근사값은 13 정도로 나왔습니다

공학용 계산기의 결과와 비교하면 오차는 7.085536919999999로 ln과 비교하면 매우 큰 값이 나왔습니다

 

어떤 값이 더 정밀하게 예측이 된 것인지 앞에서 비교한 절대오차 말고 상대오차로 비교해보겠습니다

 

상대오차는 절대오차를 참 값으로 나눈 값입니다

 

3가지 함수의 근사값의 상대오차는 아래표와 같습니다

 

함수명이 아닌 class 명으로 표를 만들었습니다

 

lns	-0.00024292823056259804
ex	0.35276811111505
sinx	-0.7401311663017484

 

절대 오차만을 보면 ex가 sinx보다 더 정밀하게 근사가 되지 않은 것 같지만

 

상대오차를 보면 오히려 sinx의 근사값이 더 정밀하지 못하다는 것을 알 수 있습니다

 

lns는 -0.00024 정도로 꽤 정밀하게 근사가 된 모습입니다

---

오늘은 이렇게 테일러 급수를 구현하고 절대오차와 상대오차를 비교하여 근사의 정밀한 정도까지 파악해 봤습니다

 

다음 포스팅은 딱히 정해두지는 않았지만 제가 공부중인 책에서 다양하게 해보겠습니다

 

긴 글 읽어주셔서 감사합니다!