작업 4와 이어집니다
저번 작업까지 표준정규분포를 그리면서 bins와 sample수를 바꿔가며
분석해봤죠
이번에는 density, 확률 밀도라고 하는 메소드를 설정해 보겠습니다
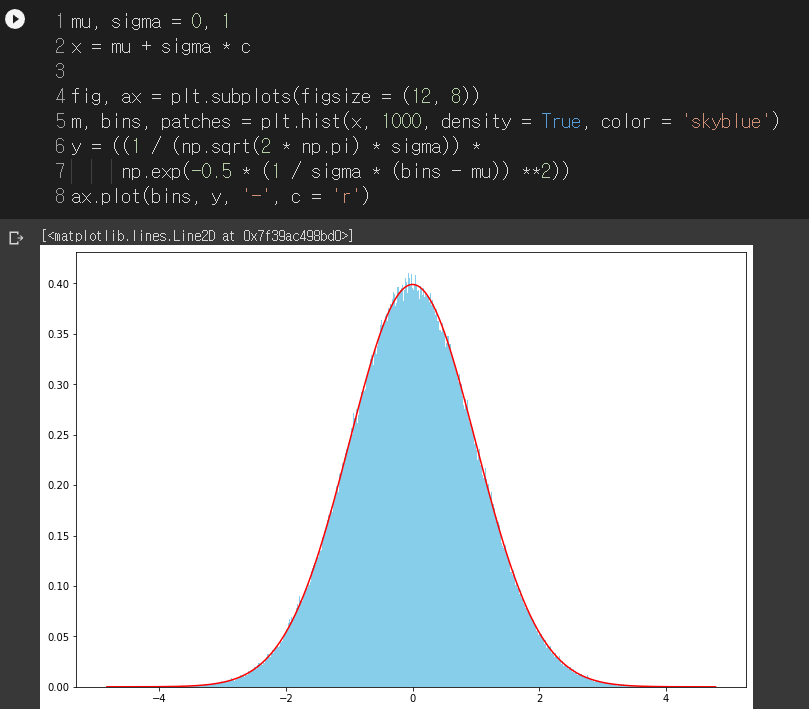
보기 쉽게 표준 정규 분포 식을 사용해서 라인도 그려봤습니다
제가 그린 히스토그램과 거의 일치하죠?

이거는 작업 4에서 그렸던 히스토그램입니다
다른 점이 보이시나요?
눈썰미 좋으신 분들은 찾으셨을거 같아요
y축이 달라지지 않았습니까?
적업 4 그래프는 4000, 3500, 3000 이렇게 가다가
density 하나만 켰을 뿐인데 0.40, 0.35 이렇게 바뀝니다
왜 그럴까요?
이건 density의 정의를 보면 알 수 있습니다
density는 밀도라는 뜻으로 확률에서 확률 밀도라고 부릅니다
확률 밀도는 그 구간의 도수 / 전체 도수 를 뜻합니다
한마디로 전체중에 이 구간이 차지하는 비율을 말하는 겁니다
근데 이제 저 사진을 보다보니 이상한 점이 하나 있었습니다
제가 그려놓은 파란선을 보시면 4000을 넘지 않죠?
4000으로 쳐서 계산해보아도 전체가 100만개니까 4000 / 1000000을 하면
0.004가 나와야 하는데 density 그림에서는 0.4가 나오는겁니다
그래서 하나하나 알아보기로 했습니다
이거는 히스토그램의 또 하나의 성질을 알아보면 쉽게 알 수 있습니다
히스토그램에 모든 직사각형의 넓이의 합이 1인걸 이용하면 쉽게 알 수 있습니다
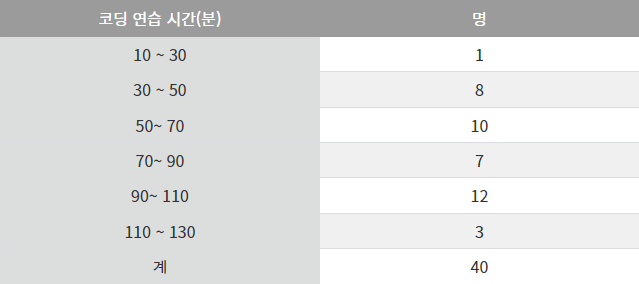
이건 작업 4에서 그렸던 표입니다
확률 밀도를 도수분포표에 적용을 시킬때는 다른 용어로 사용이 됩니다
한 번 쯤은 들어봤던 상대도수라는 용어가 사용이 됩니다
용어만 다를뿐 똑같은 말 입니다
구간들의 모든 도수들을 합하면 계와 같듯이
상대 도수는 전체를 1로 두었을 때 어느정도냐를 상대적으로 따지는 것입니다
그렇기 때문에 상대도수들을 전부 합하면 1이라는 값이 나오는 것도 쉽게 알 수 있습니다
위에 표를 통해 구해봅시다
1/ 40, 8/ 40, 10/ 40, 7/ 40, 12/ 40, 3 / 40 이렇게 계산을 해보면
0.025, 0.2, 0.25, 0.175, 0.3, 0.075 이렇게 나옵니다
이것들을 다 합해보면? 1이 나옵니다
위에서 봤던 것과 비슷하지 않나요?
상대도수를 전부 합하면 1이다, 히스토그램의 모든 직사각형의 넓이의 합은 1이다
이걸 통해 우리는 히스토그램의 직사각형의 넓이가 의미하는게 상대도수라는 걸 알아낼 수 있습니다
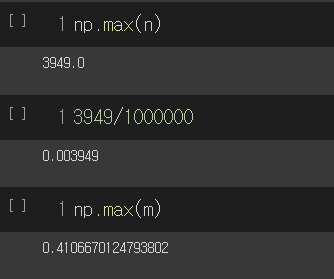
제가 그린 표준 정규 분포 그림에서도 증명해보겠습니다
n은 density를 키지 않은 그림입니다
저 그림의 최대값은 3949입니다
이걸 전체로 나누면 0.003949라는 값이 나와야 하지만
density를 키고 그린 그림의 최대값은 약 0.41이라는 값이 나옵니다
다시 히스토그램으로 넘어가서
히스토그램의 직사각형의 넓이가 상대도수다
그러면 상대도수 = 밑변 * 높이 이런 식으로도 쓸 수 있겠죠?
히스토그램에서 밑변은 구간의 폭, 높이는 y축에 있는 숫자들이었죠
그렇기 때문에 y축에 숫자 = 상대도수 / 구간의 폭 을 한 숫자라는 결론이 나옵니다
맞는지 한 번 볼까요?

먼저 구간 1개의 폭을 구하기 위해서 최댓값과 최솟값을 구해서 bins의 갯수로 나누어줍니다
그러면 bins 1개의 폭은 약 0.0096이라는 걸 알았습니다
그리고 상대도수를 구해야 하죠?
상대도수는 이미 위에서 구했습니다
3949를 1000000으로 나눈 수 0.003949
상대도수는 구간의 폭으로 나누어보면
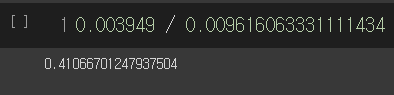

density를 키고 그린 그림의 값과 거의 일치하지 않나요?
기계적인 계산 오차는 늘 있을 수 있습니다
0.410667012379 이정도 까지 맞으면 기계는 거의 일치하는 값으로 인식을 하기 때문에
소수점 너무 아랫자리가 틀리다고 해서 다른 값은 아닙니다
그러면 마지막
density를 켠 히스토그램이 진짜 넓이들의 합이 1인지 봐보겠습니다
방법은 y축의 값들을 모두 더해서 구간의 폭으로 나누어 주면 되겠죠?
해보면
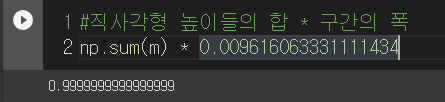
컴퓨터는 사용자가 보기 편하게 출력을 하기 때문에
순환소수여도 어느 정도 선까지만 출력을 합니다
결과적으로 이 값은 0.9999... 이어지는 순환소수이고
중고등학교 때 배운 순환소수 개념을 사용해보면 1이라는 것을 알 수 있습니다
신기하지 않나요?
이렇게 하나하나 증명해보는게 생각보다 재미가 있어요!
내가 아니라 컴퓨터가 그리게하고 컴퓨터가 계산하게 하며
코딩 능력도 키울 수 있구여
표준 정규 분포 작업은 여기까지가 될 거 같습니다
다음 작업은 아마 강수량 자료를 가지고 해볼까 합니다
아직은 확정된 것은 없구여
데이터 시각화가 목표가 아니라
데이터 분석이 목표이기 때문에 이제는 단순 시각화를 넘어서서
그려보고 제 나름대로 분석을 해보려고 합니다
'파이썬' 카테고리의 다른 글
| 작업7 : Python을 통한 GUI 프로그래밍2 (0) | 2022.10.18 |
|---|---|
| 작업6 : Python을 통해 GUI 프로그래밍 1 (0) | 2022.10.18 |
| 작업 4 : 표준 정규 분포 그려보기 (0) | 2022.04.08 |
| 작업 2 : Folium으로 울진 산불 지도에 표시해보기 (0) | 2022.03.22 |
| Matplotlib를 시작해보자 (0) | 2021.11.02 |