오늘은 태양의 적위를 계산해보겠습니다

먼저 적위가 뭔지 알아볼께여
적위를 이해하기 위해선 천구라는 것부터 알아야합니다
천구는 관측자나 지구를 중심으로 반지름이 무한대인 커다란 구를 말합니다
별들이 이 천구에 박혀있다라는 표현을 쓰기도 합니다
천구 안의 지구는 자전축이 23.5 도 기울어진채 자전을 합니다
지구의 적도에서 천구로 적도를 무한히 확장했을 때 생기는 원을 천구의 적도라고 합니다
본론으로 돌아와서 그럼 적위는 무엇일까요??
천구의 적도와 태양이 이루는 각을 적위라고 합니다
말로만 하면 이해가 어려우니 그림을 가져올께여


위의 사진을 보시면 이해가 되실 겁니다
저번 포스팅에서 이심률을 계산하는 공식이 2개라고 했었는데 적위는 1개 더 많은 3개나 됩니다
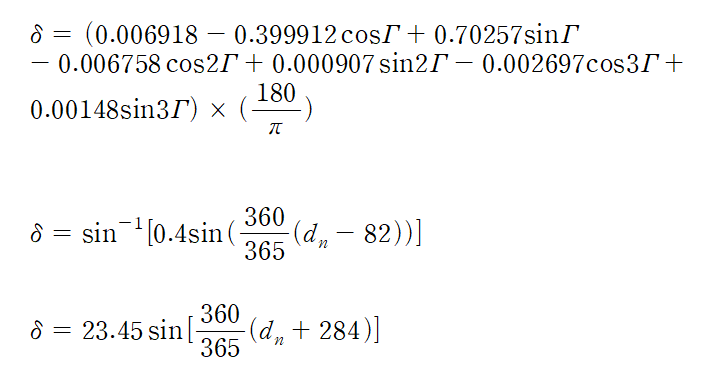
이렇게 3개나 됩니다
길어보이지만 충분히 할 수 있습니다
단순한 공식만 쓰면 해결이 됩니다
하나씩 해보겠습니다
1번 공식)
REAL :: r, d
REAL, parameter :: pi = 4. * atan(1.)
open(1, file = 'sd1.csv')
do i = 1, 365
r = (2 * pi * (i - 1))/365
d1 = 0.006918 - 0.399912*cos(r) + 0.070257*sin(r) - 0.006758*cos(2*r)
d2 = 0.000907*sin(2*r) - 0.002697*cos(3*r) + 0.00148*sin(3*r)
d = (d1 + d2) * (180/pi)
write(1, 10) i,',',d
10 format(i3, a, f10.2, a)
end do
end
1번 공식에서 설명드릴 점은 각도를 대입할 때 각도법에서 라디안으로 바꿔서 넣어줘야 한다는 점 인 것 같습니다
저희가 일반적으로 쓰는 각도법은 컴퓨터가 인식을 하지 못합니다
꼭 각도에 이걸 곱해야 라디안으로 입력이 되고 컴퓨터가 계산을 할 수 있게 됩니다

r은 저번 포스팅에서 썼던 감마라는 변수입니다
여기서 이미 파이가 곱해져서 계산이 되기 때문에 따로 라디안으로 바꿔주지 않아도 됩니다
하지만 결과를 각도법으로 보기 위해서는
이 친구를 곱해주어야 각도법으로 출력이 됩니다
라디안으로 바꾸기 위해서는 pi/180, 각도법으로 바꾸기 위해서는 180/pi를 곱해야 하는거 꼭 명심하세요!
나머지는 단순한 공식과 설명 드렸던 내용들이기 때문에 넘어가겠습니다
2번 공식)
REAL :: d, r
REAL, parameter :: pi = 4. * atan(1.)
open(1, file = 'sd2.csv')
write(1, *)'dn',',','dc'
do i = 1, 365
r = ((360./365.) * (i - 82.)) * (pi/180)
d1 = asin(0.4 * sin(r))
d = d1 * (180./pi)
write(1, 10) i,',',d
10 format(i3, a, f10.2, a)
end do
end2번 공식도 제 포트란 기초 포스팅을 보고 오셨다면 크게 문제는 없습니다
이걸 어떻게 입력시키나 하실수도 있을 것 같습니다
수학에서 sin, cos, tan라고 부르는 삼각함수들의 역함수는
앞에 arc를 붙여서 arcsin, arccos, arctan으로 부릅니다
너무 기니까 포트란에서는 asin, acos, atan으로 사용합니다
여기서 이제 처음으로 r = ((360./365.) * (i - 82.)) * (pi/180) 라디안으로 바꾸는 부분이 나옵니다
이 부분 전체가 sin 안으로 들어가기 때문에 꼭 바꿔주어야 합니다
눈썰미가 좋으신 분들은 asin으로 다시 한 번 들어가는데 여기는 왜 pi/180을 곱해주지 않나요? 하실수도 있습니다
한 번 라디안 값으로 계산이 되었기 때문에 이후의 모든 값들은 라디안 방식으로 계산됩니다
여기도 d = d1 * (180./pi) 각도법으로 꼭 바꿔주어야 하구요
3번 공식)
REAL :: d
REAL, parameter :: pi = 4. * atan(1.)
open(1, file = 'sd3.csv')
write(1, *)'dn',',','dc'
do i = 1, 365
d = 23.45 * sin(((360./365.) * (i + 284)) * (pi/180))
write(1, 10) i,',',d
10 format(i3, a, f10.2, a)
end do
end
3번 공식은 앞에 두 공식을 혼자서 잘 쓰셨다 하시는 분들은 충분히 해내셨을거라고 믿습니다
3번 공식에 가장 쉽기 때문입니다
제 코드들을 보면 공간이 남는데도 f10.2를 많이 쓰는데 이 부분은 학교에서 첨 배울때 f10.2로 배워서 습관적으로 쓰는 거기 때문에
여러분들이 보기 편한 방식으로 충분히 바꾸시면 될 것 같습니다
포트란은 하는 분들도 별로 없고 대기과학 분야가 아니면 거의 사용하지 않기 때문에 단순히 코드만 올려놓으려고 했습니다
하지만 오히려 포트란을 더 대중화시킬 수 있지 않을까? 하는 생각이 문득 들었습니다
포트란만큼 쉽고 강력한 언어가 몇개 없다고 생각합니다
정말 직관적이고 빠르고 단순하기 때문에 문법 몇개만 배우면 쉽게 하실 수 있는 언어라고 생각합니다
'대기과학에서만 쓰는 언어다' 라기 보다는 쉽고 강력한 언어로 여러분들에게 기억이 되고
코딩을 처음 접하시는 분들도 포트란을 너무 어렵게 대하지 않으셨으면 좋겠습니다
꼭 포트란을 한 번 짬은 해보시면 좋을 것 같습니다
'Fortran' 카테고리의 다른 글
| 작업6 : Fortran으로 합성 풍속 풍향 구하기2 (0) | 2022.10.26 |
|---|---|
| 작업5 : Fortran으로 합성 풍향 풍속 구하기1 (0) | 2022.10.26 |
| 작업4 : Fortran으로 시간방정식 계산하기 (0) | 2022.10.26 |
| 작업2 : 이심률 구하기 (3) | 2022.10.18 |
| 작업1 : 태양의 유효복사온도 계산 (0) | 2022.10.18 |