어제도 제 블로그를 찾아주신 일곱 분 감사드립니다!
오늘은 t분포와 p-value, 확률 밀도 함수에 대해 더 자세히 알아보겠습니다

저번에 이제 선형 회귀 분석에서 결정계수와 p-value가 의미하는 것을 확인해봤습니다
p-value를 제대로 사용하려면 먼저 student - t분포에 대해 알아야 합니다
원래 t-value는 모집단의 표준편차를 모르는 경우 표본의 표준편차를 가지고
모집단의 표준편차를 추정할 때 사용하는 값 입니다
t-value 공식은 다음과 같습니다

제가 배운 방법으로는 상관계수를 검증하는 부분에서 나오기 때문에 상관계수를 이용해서 구합니다

상관계수를 구하는 공식은 이렇습니다
n-2는 자유도를 의미합니다
t-value는 2개의 모수가 추정이 가능하기 때문에 n-2가 된다고 알려져 있습니다
자료의 갯수가 20개면 자유도는 18, 자료의 갯수가 100개면 자유도는 98, 이렇게 계산하면 됩니다
자 그러면 자유도가 20일 때의 상황을 가정해봅시다
그러면 t-value를 구하는 식은 온전히 상관계수에 대해서만 구해지게 됩니다

오직 상관계수의 범위 -1부터 1 사이 내에서만 계산이 됩니다
주어진 범위 내에서 모든 실수에 대해지는 변수들을 그려낸 분포를 확률 밀도함수라고 부릅니다
확률 질량 함수는 분포에서 막대 길이 자체가 확률이지만
확률 밀도 함수에서는 넓이를 의미합니다
-INF 부터 +INF인 범위 내에서

a부터 b사이에서 사건이 일어날 확률은 적분을 통해구하게 됩니다
* 여기서 f(t)는 확률 함수 입니다
그러먼 우리가 구하는 t-value도 연속적인 상관계수 범위 내에서 구해지는 값이니
분포를 그리면 확률 밀도함수 형태로 나오겠죠??
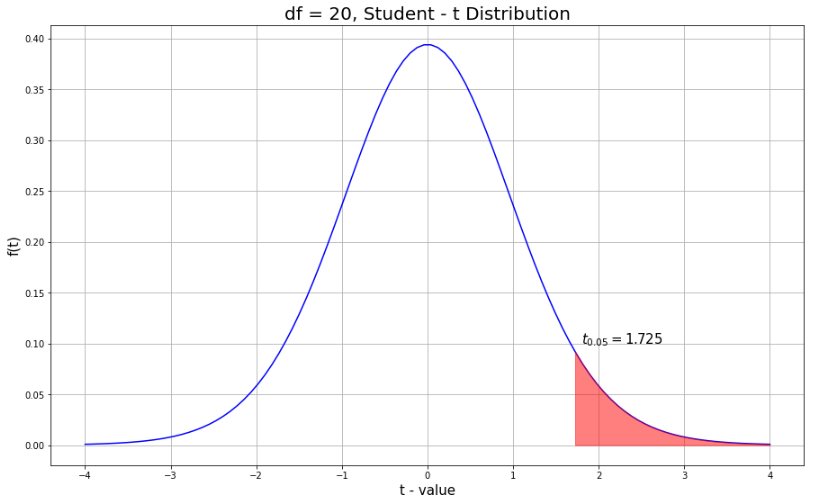
그래서 제가 바로 그려본 자유도가 20일 때의 t분포 입니다
물론 자유도가 몇이던 상관 없이 양쪽 끝은 - INF 와 +INF입니다
상관 계수가 -1이나 1일때는 분모가 0이 되기 때문에 발산하기 때문이죠
그렇기 때문에 분포가 너무 커지면 모양을 보기 힘들기 때문에 -4부터 4까지만 제한해서 그렸습니다
그림에 제가 표시한 부분이 자유도가 20일 때 기각역 입니다
기각역은 귀무가설이 기각되고 대립 가설이 채택되는 영역을 말합니다
저는 단측검증만을 진행했습니다
배운 부분에서는 단측검정만 사용했기 때문에 양측 검증이 필요한 부분이 나오면
추가해서 바로 포스팅 하겠습니다
여기서 중요한 점은 위에 t-value 공식을 다시 살펴보겠습니다

자 이 공식입니다
이 공식에서 알 수 있는 중요한 사실이 하나 있습니다
바로 t-value와 상관계수가 비례한다는 겁니다
student - t 분포를 보면 양 옆으로 갈수록 t 값이 커지는 걸 볼 수 있습니다
그렇다는건 양극으로 갈수록 상관계수도 같이 커진다는 말 입니다
이 점을 잘 알고 계속 가보겠습니다
바로 앞 포스팅에서 p-value를 설명할 때 유의수준이라는 개념이 나왔습니다
유의수준이 5% 라는 얘기는
확률 밀도 함수에서 일부를 적분한 값, 즉 범위 내의 면적의 넓이가 0.05라는 말입니다
확률 밀도 함수도 확률을 구하는 개념이기 때문에 -INF부터 INF 까지 적분한 넓이는 1이 나옵니다

다시 이 그림에서 보면
제가 그림에 적어 놨듯이 빨간 부분이 시작되는 영역이 t 0.05
즉, 자유도가 20인 t분포에서 t값이 1.725부터 +INF까지 적분한 넓이가 0.05라는 뜻입니다
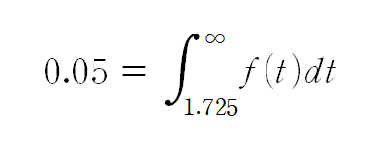
여기서 1.725라는 값은 t분포표에서 알 수 있습니다

이렇게 찾아집니다
위에 알파 부분이 유의수준, df가 자유도입니다
저렇게 적분되어져 나오는 영역이 확률이라고 했죠??
저 영역의 넓이를 p-value라고 부르는 겁니다
자유도가 20인 t분포에서 p-value가 0.05가 나오려면 사용해야하는 t값이 1.725라는 말입니다
자 이제 다 왔습니다
위에서 나열한 내용들을 다시 정리해보겠습니다
- t분포는 확률 밀도 함수다 (자유도를 정하고 나면 상관계수에 의해서만 구해진다)
- t값과 상관 계수 r은 비례한다
- t분포를 적분한 값이 p-value이다
이렇게 정리가 됩니다
그러면 내가 구한 t값이 1.725보다 크면? 저 영역의 넓이가 빨간색 보다 작아지겠죠?

이 그림처럼 됩니다
검은 부분은 t = 2일 때 영역을 색칠한 겁니다
그러면 구한 t값이 유의수준 t값보다 크다 라는 말은
내가 구한 상관계수가 유의수준 상관계수보다 크다는 말과 같죠??
그러면 내 상관계수가 유의하다고 정의할 수 있는 겁니다
반대로 영역이 유의수준보다 커지면?
t값이 작게 나온거고 상관계수도 작기 때문에 유의하지 못하다 라고 정의됩니다
최종정리
- 구한 영역이 더 작다 -> t값이 더 크게 나왔다 -> 상관계수가 더 크게 나왔다 -> 상관계수가 유의하다
- 구한 영역이 더 크다 -> t값이 더 작게 나왔다 -> 상관계수가 더 작게 나왔다 -> 상관계수가 유의하지않다
(구한 영역 = p-value, p-value가 유의수준보다 작은지 큰지를 비교하는 과정)
이런 방식으로 상관계수 검증을 진행합니다
회귀 계수 검증은 다른 방법이 있기 때문에 뒤에가서 다시 설명드리겠습니다
방식은 똑같고 t값을 구하는 방식이 다를 뿐입니다
오늘도 긴글 읽어주셔서 감사합니다
'통계' 카테고리의 다른 글
| MSE, MSR 의미 알아보고 F비 파이썬으로 구해보기 (0) | 2022.12.31 |
|---|---|
| 상관계수와 회귀식, 예측값 파이썬으로 구해보기 (2) | 2022.12.21 |
| 상관 계수 5%, 1% 수준 유의성 검사 파이썬으로 해보기 (0) | 2022.12.20 |
| 결정계수와 p-value 파이썬으로 구해보기 (0) | 2022.12.09 |