오늘은 과제로 나왔던 EBM 기후모델을 만들어보겠습니다

먼저 EBM 모델에 대해 간단하게 설명하겠습니다
제가 배운 내용으로는 기후모델은 크게 4가지가 있습니다
- Energy Balance Models
- One-Dimensional Radiative-convective Models
- Two-Dimensional Statistical-Dynamical Models
- Thress-Dimensional General Circulation Models
저는 여기서 맨 앞에 있는 Energy Balance Models을 만들어보겠습니다
줄여서 EBM이라고 부르겠습니다
EBM은 이 기후 시스템에서 적용되는 열역학 제 1법칙만을 나타냅니다
주변 환경과 물질이나 공간을 교환하지 않기 때문에 닫힌 열역학 시스템입니다
시간 척도를 1년, 1일, 1시간 처럼 다양하게 할 수 있지만 저는 연간 시스템, 1년 단위로 만들겠습니다

공식은 이렇게 생겼습니다
이 공식에서 상수는
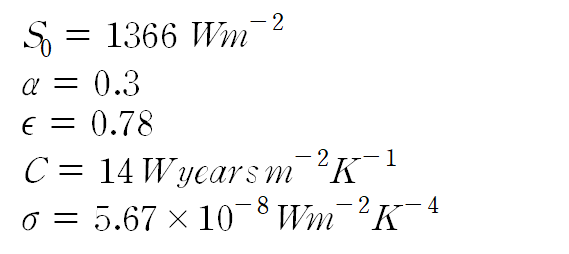
순서대로 태양상수, 알베도, 방출률, 지구의 열용량, 스테판-볼츠만 상수입니다
여기서 바뀌는 태양상수, 알베도, 방출률입니다
- 태양이 방출하는 태양 에너지가 증가한다
- 지구가 반사를 더 많이 시킨다
- 대기가 자신이 가진 열을 더 많이 방출한다
태양 에너지가 증가하는 것은 지구의 표면온도를 더 뜨겁게 만들고
방출율이 증가하면 대기가 자신이 가진 열을 더 많이 방출하는 것이기 때문에 이 역시 지구 표면온도가 뜨거워집니다
알베도는 지구의 반사율이기 때문에 반사율이 커지면 표면온도는 낮아집니다
오른쪽 공식의 해를 구해야 합니다
미분 방정식 형태이기 때문에 해를 구하려면 4th Runge - Kutta intergration method를 사용합니다
이 식을 설명드리기에는 조금 어려운 식이라 간단하게만 설명드리고 넘어가겠습니다
왼쪽 항에서 지구 표면온도는 시간의 따른 변수이기 때문에 이 값을 근사하기 위한 방법입니다


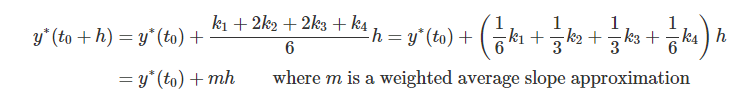
공식자체도 되게 복잡하게 생겼습니다
더 자세한 내용이 궁금하신 분은 아래 링크에서 확인해 보셔두 됩니다
https://lpsa.swarthmore.edu/NumInt/NumIntFourth.html
Fourth Order Runge-Kutta
Fourth Order Runge-Kutta Contents Introduction In the last section it was shown that using two estimates of the slope (i.e., Second Order Runge Kutta; using slopes at the beginning and midpoint of the time step, or using the slopes at the beginninng and en
lpsa.swarthmore.edu
저 식을 파이썬으로 구해내는 것이 목표입니다
먼저 초기 조건들입니다
s0 = 1366
si = 5.67e-8
ep = 0.78
al = 0.3
c = 14
t0 = 0
tn = 50
ntime = 50
dt = (tn - t0)/ntime
hdt = dt/2
ts0 = 0
cell0 = t0
cell2 = ts0기간은 50년으로 설정했습니다
나머지는 주어진 조건들이라 똑같이 작성하시면 될 것 같습니다
다음은 구현하는 코드입니다
bet = []
for i in np.arange(0, 51, 1):
k11 = dt*(((1-al)*s0/4 - si*(1-ep/2)*globals()["cell{}".format(i)]**4)/c)
y22 = globals()["cell{}".format(i)] + k11/2
k22 = dt*(((1-al)*s0/4 - si*(1-ep/2)*y22**4)/c)
y33 = globals()["cell{}".format(i)] + k22/2
k33 = dt*(((1-al)*s0/4 - si*(1-ep/2)*y33**4)/c)
y44 = globals()["cell{}".format(i)] + k33
k44 = dt*(((1-al)*s0/4 - si*(1-ep/2)*y44**4)/c)
globals()["cell{}".format(i + 1)] = globals()["cell{}".format(i)] + (k11 + 2*k22 + 2*k33 + k44)/6
bet.append(globals()["cell{}".format(i + 1)])50개의 변수가 필요했기 때문에 globals()를 이용해서 만들었습니다
그 후에 bet라는 리스트에 넣었습니다
시간에 따라 표면 온도가 어떻게 변하는지 보고 싶은 것이기 때문에 그래프가 있으면 편하겠죠??
dx = np.arange(0, 51, 1)
fig, ax = plt.subplots(figsize = (17, 12))
ax.plot(dx, bet, color = "red", lw = 3)
ax.axhline(cell50, color = "blue", lw = 2)
ax.set_title("Time Evolution of Earth's Surface Temperature \n by 0-Dimensional EBM",
fontsize = 25)
ax.set_xlabel("Time (Year)", fontsize = 20)
ax.set_ylabel("Temperature (K)", fontsize = 20)
ax.yaxis.set_major_locator(MultipleLocator(40))
ax.xaxis.set_major_locator(MultipleLocator(10))
ax.xaxis.set_minor_locator(MultipleLocator(1))
ax.yaxis.set_minor_locator(MultipleLocator(20))
plt.xticks(fontsize = 15)
plt.yticks(fontsize = 15)
ax.set_ylim(0,320)
ax.set_xlim(0, 50)
plt.text(40, 80, '$\epsilon_{1} = 0.78$', fontsize = 30)
plt.text(40, 65, 'Max = 288.3128', fontsize = 15)강의 노트에 예시 그림이 있어서 최대한 똑같이 그렸습니다
50년이기 때문에 np.arange로 만들었습니다
초기 조건을 보면 t0가 0년이기 때문에 np.arange로 만들때도 1부터가 아니라 0부터 뽑았습니다
이렇게 그림을 그려보면

이런 그림이 나오게 됩니다
20년 정도 가파르게 증가하다가 40년이 지나면 그래프가 거의 수평에 가까워집니다
제가 그린 파란색 수평선은 이 그래프에서 가장 최대값인 288.3128로 그렸습니다
미분 방정식은 어떻게 변화하는지를 지정한 방정식이며 초기 조건이 주어졌을 때, 시스템이 시간에 따라 변화하게 만들기
때문에 초기 온도와 초기 시간이 0년, 0K로 주어졌고, 기타 초기 조건들에 따라 온도가 어떻게 변하는지 구한 것입니다
조금 더 자세한 설명은 다음 포스팅에서 말씀드리겠습니다!
(아직은 그래프의 의미 공부가 더 필요할 것 같아요..)
다음 포스팅에서는 이산화탄소 농도가 2배일 때의 변화와 방출률에 따른 변화를 알아보겠습니다
긴 글 읽어주셔서 감사합니다!!
'파이썬' 카테고리의 다른 글
| 작업26: 파이썬으로 대기 상단 연평균 일사량 계산하고 시각화하기1 (0) | 2023.04.30 |
|---|---|
| 작업17: Python으로 EBM 기후모델 만들기2 (0) | 2023.01.06 |
| 작업 15: Python으로 선형 회귀 모델 적합성 검사 라이브러리 만들기2 (2) | 2022.12.31 |
| 작업 14: Python으로 선형 회귀 모델 적합성 검사 라이브러리 만들기1 (0) | 2022.12.06 |
| 작업13: Python으로 부산 평균 최고기온 분석하기 4 (0) | 2022.12.04 |