저번 포스팅에 이어서 기후모델이 다양한 조건들을 넣어 결과를 확인해 보겠습니다

이전 포스팅에서 기후모델을 Runge-kutta 4차 방법으로 만들어봤었습니다
과제로 나왔던 조건들을 넣으면서 예상 결과와 어떻게 다른지 확인해보겠습니다
먼저 첫 번째 입니다
1. Try changing ϵ=0.78 to ϵ=0.80 in the code provided. (It is noticeable that this change in emissivity of the atmosphere can occur due to doubled CO2 concentration)
= 방출률을 0.78에서 0.8로 바꿔보십쇼(이는 이산화탄소 농도가 2배로 증가했을 때 발생할 수 있다)
코드에서 기본으로 주어진 상태에서 0.78로 설정했던 방출률을 0.8로 바꾸보는 겁니다
대기 중 이산화탄소 농도가 2배로 증가하면 방출률이 0.8로 증가한다고 합니다
코드로 만들어보겠습니다
s0 = 1366
si = 5.67e-8
ep2 = 0.8
al = 0.3
c = 14
t0 = 0
tn = 50
ntime = 50
dt = (tn - t0)/ntime
hdt = dt/2
ts0 = 0
cel0 = t0
cel2 = ts0초기 조건들 입니다
다른 것들은 전부 똑같고 방출률만 0.8로 바꿔줬습니다
gam = []
for i in np.arange(0, 51, 1):
k11 = dt*(((1-al)*s0/4 - si*(1-ep1/2)*globals()["cel{}".format(i)]**4)/c)
y22 = globals()["cel{}".format(i)] + k11/2
k22 = dt*(((1-al)*s0/4 - si*(1-ep1/2)*y22**4)/c)
y33 = globals()["cel{}".format(i)] + k22/2
k33 = dt*(((1-al)*s0/4 - si*(1-ep1/2)*y33**4)/c)
y44 = globals()["cel{}".format(i)] + k33
k44 = dt*(((1-al)*s0/4 - si*(1-ep1/2)*y44**4)/c)
globals()["cel{}".format(i + 1)] = globals()["cel{}".format(i)] + (k11 + 2*k22 + 2*k33 + k44)/6
gam.append(globals()["cel{}".format(i + 1)])계산 구현도 동적으로 만들어진 변수 이름만 cell{}에서 cel{}로 변경해주고 나머지는 똑같습니다
fig, ax = plt.subplots(figsize = (17, 12))
ax.plot(dx, alp, color = "red", lw = 3)
ax.axhline(ce50, color = "blue", lw = 2)
ax.set_title("Time Evolution of Earth's Surface Temperature \n by 0-Dimensional EBM",
fontsize = 25)
ax.set_xlabel("Time (Year)", fontsize = 20)
ax.set_ylabel("Temperature (K)", fontsize = 20)
ax.yaxis.set_major_locator(MultipleLocator(40))
ax.xaxis.set_major_locator(MultipleLocator(10))
ax.xaxis.set_minor_locator(MultipleLocator(1))
ax.yaxis.set_minor_locator(MultipleLocator(20))
plt.xticks(fontsize = 15)
plt.yticks(fontsize = 15)
ax.set_ylim(0,320)
ax.set_xlim(0, 50)
plt.text(40, 80, '$\epsilon_{1} = 0.80$', fontsize = 30)
plt.text(40, 65, 'Max = 289.5057', fontsize = 15)이전 포스팅과 똑같이 그림을 그리면
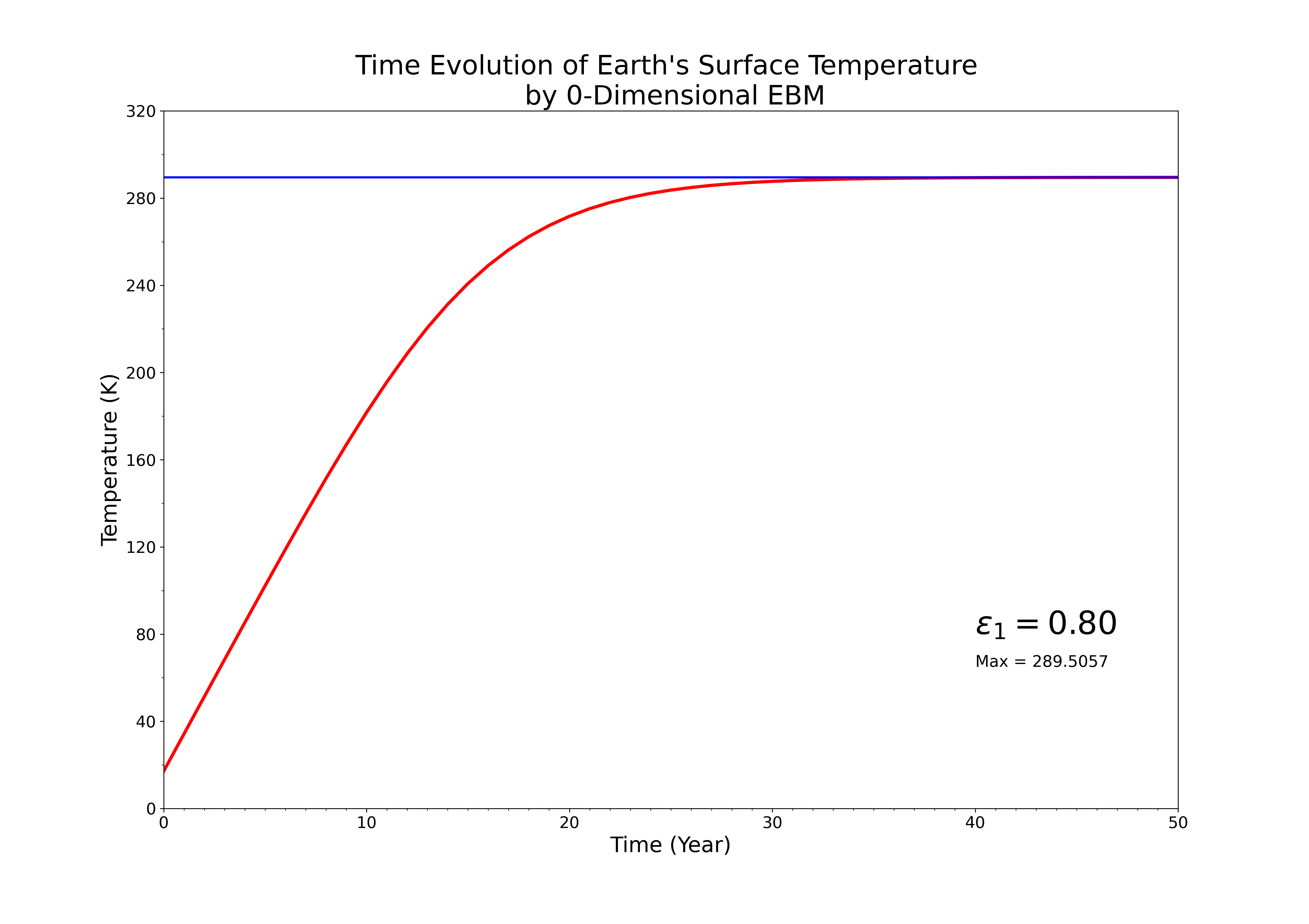
이렇게 그림이 나옵니다
방출률이 0.8로 증가하면 지구 표면온도가 289.5057K로 증가한 모습을 볼 수 있습니다
이전 포스팅에서 계산값인 288.3128보다 약 1.2K 정도 상승한 모습입니다
다음 문제에서 조금 이상한 점이 확인됩니다
2. According to IPCC, a typical prediction from the GCMs is 3K surface warming under doubling of CO2 concentration. Explain the possible reason of the underestimated warming by this simple EBM
= IPCC에 따르면 General Circulation Models에서 이산화탄소 농도가 2배 증가하면 지구 표면온도가 3K
증가한다고 예측됩니다
간단한 EBM모델에서 3K 상승하지 않은 가능한 이유를 설명하시오
3차원 모델인 GCMs에서 이산화탄소 농도가 2배 증가하면 3K가 증가한다고 예측하지만
제가 만들어본 0차원 Energy Balance Models 에서는 1.2K 정도 밖에 증가하지 않았습니다
왜 일까요??
이는 0차원 EBM은 대기 흐름이나 , 역학, 복사 법칙들을 전혀 고려하지 않은 모델이기 때문입니다
대기와 해양이나 대기와 육지처럼 서로 영향을 주는 요인들이 많은데 이런 것들은 전부 고려하지 않았기 때문입니다
서로 다른 요인들이 영향을 주면서 기존에 현상들을 가속화 시키거나 느리게 감속 시키는
현상을 기후 피드백이라고 합니다
이는 예시로 보면 되게 쉽게 이해가 가능합니다
먼저 지구가 점점 뜨거워지면서 해양의 열 흡수가 증가하는 현상부터 시작해보겠습니다
해양의 열 흡수가 증가하면 해수 온도가 증가합니다
해빙들은 여름에는 녹고 겨울에 어는 과정을 반복하면서 면적을 유지하려고 하지만
해수 온도가 증가하면 해빙이 녹는 기간이 길어지게 됩니다
그러면 해빙의 면적이 유지되지 못하고 점점 줄어들게 되고
이로 인해 해양의 반사도가 감소하면서 다시 해양의 열 흡수 증가로 돌아오게 됩니다
그림으로 보면

이러한 과정을 계속 거치면서 해수온도 증가와 열 흡수 증가 속도가 점차 가속화 됩니다
어런 과정을 거치며 가속되거나 감속되는 것을 기후 피드백이라고 합니다
3차원 GCMs는 기후 피드백 현상까지 고려한 온도 증가율이기 때문에 3K 가량 증가한다고 예측한 것입니다
마지막 문제는 답을 알려주셨습니다
3. Find that how much additional increase of ϵ is needed to approximate the GCMs’ prediction
(i.e. 3K)
= EBM 모델로 3K가 증가하려면 방출률이 얼마까지 증가해야 하는지 찾으시오
방출률이 0.83까지 증가하면 약 3K 증가한다고 알려주셨습니다
위와 똑같이 EBM 모델을 통해 계산하고 그림을 그려봤습니다
s0 = 1366
si = 5.67e-8
ep1 = 0.83
al = 0.3
c = 14
t0 = 0
tn = 50
ntime = 50
dt = (tn - t0)/ntime
hdt = dt/2
ts0 = 0
ce0 = t0
ce2 = ts0
alp = []
for i in np.arange(0, 51, 1):
k11 = dt*(((1-al)*s0/4 - si*(1-ep2/2)*globals()["ce{}".format(i)]**4)/c)
y22 = globals()["ce{}".format(i)] + k11/2
k22 = dt*(((1-al)*s0/4 - si*(1-ep2/2)*y22**4)/c)
y33 = globals()["ce{}".format(i)] + k22/2
k33 = dt*(((1-al)*s0/4 - si*(1-ep2/2)*y33**4)/c)
y44 = globals()["ce{}".format(i)] + k33
k44 = dt*(((1-al)*s0/4 - si*(1-ep2/2)*y44**4)/c)
globals()["ce{}".format(i + 1)] = globals()["ce{}".format(i)] + (k11 + 2*k22 + 2*k33 + k44)/6
alp.append(globals()["ce{}".format(i + 1)])
fig, ax1 = plt.subplots(figsize = (17, 12))
#plot
ax1.plot(dx, gam, color = "red", lw = 3)
#axis label and title
ax1.set_title("Time Evolution of Earth's Surface Temperature \n by 0-Dimensional EBM",
fontsize = 25)
ax1.set_xlabel("Time (Year)", fontsize = 20)
ax1.set_ylabel("Temperature (K)", fontsize = 20)
#axis tick parameter
ax1.yaxis.set_major_locator(MultipleLocator(40))
ax1.xaxis.set_major_locator(MultipleLocator(10))
ax1.xaxis.set_minor_locator(MultipleLocator(1))
ax1.yaxis.set_minor_locator(MultipleLocator(20))
ax1.tick_params(which = 'minor', length = 5)
ax1.tick_params(which = 'major', length = 7)
plt.xticks(fontsize = 15)
plt.yticks(fontsize = 15)
#axis limit
ax1.set_ylim(0,320)
ax1.set_xlim(0, 50)
plt.text(40, 80, '$\epsilon_{2} = 0.83$', fontsize = 30)
plt.text(40, 65, 'Max = 291.3428', fontsize = 15)
이러한 그림이 나옵니다
맨 처음 계산값인 288.3128보다 약 3K 정도 증가한 그래프입니다
EBM 모델에서는 방출률이 0.83까지 증가해야만 3K가 증가한다는 것을 알 수 있습니다
이렇게 간단한 기후모델을 만들고 조건들을 바꾸면서 지구 표면온도 변화를 알아봤습니다
오늘도 긴 글 읽어주셔서 감사합니다!
'파이썬' 카테고리의 다른 글
| 작업27: 파이썬으로 대기 상단 연평균 일사량 계산하고 시각화하기2 (0) | 2023.04.30 |
|---|---|
| 작업26: 파이썬으로 대기 상단 연평균 일사량 계산하고 시각화하기1 (0) | 2023.04.30 |
| 작업16: Python으로 EBM 기후모델 만들기1 (2) | 2023.01.04 |
| 작업 15: Python으로 선형 회귀 모델 적합성 검사 라이브러리 만들기2 (2) | 2022.12.31 |
| 작업 14: Python으로 선형 회귀 모델 적합성 검사 라이브러리 만들기1 (0) | 2022.12.06 |