저번 포스팅에 이어서 대기 상단 일사량을 계산하고 시각화 해보겠습니다


저희가 해야할 건 이 공식을 계산하는 코드를 구현하면 됩니다
대기 상단 일사량은 시간각하고 똑같게 위도별로 365개를 계산해줘야합니다
과제에는 위도별 평균 일사량과 적도, 북위 30, 60, 90도에서의 그래프 이렇게 2가지를 요구하고 있기에
일반적으로 계산된 값이 나열된 자료와 평균값 이렇게 2개가 필요합니다
바로 가보겠습니다
def cal_e(phi):
ii = []
s = 1361
d1 = de
d2 = be
for i in range(len(d1)):
E = (s/np.pi) * d2[i] * (globals()['a{}'.format(phi)][i] * np.sin(np.radians(phi)) * np.sin(np.radians(d1[i]))
+ np.cos(np.radians(phi)) * np.cos(np.radians(d1[i])) * np.sin(globals()['a{}'.format(phi)][i]))
ii.append(E)
globals()['ph{}'.format(phi)] = ii
globals()['mean{}'.format(phi)] = np.array(ii).mean()대기 상단 일사량 계산도 함수형태로 만들어서 코드를 단순화 시켰습니다
계산 자체가 길기도 하고 변수명들을 globals로 만들었기 때문에 길어진 것 뿐이라서
어렵지는 않습니다
코드 구성 방식은 앞에 시간각과 전혀 다른게 없습니다
계산하고 빈 리스트에 넣는 방식으로 만들었습니다
여기서는 2번의 동적 변수를 생성합니다
하나는 계산값 나열, 나머지 하나는 평균입니다
gg = []
for y in np.arange(-90, 91, 1):
cal_e(y)
gg.append(globals()['mean{}'.format(y)])평균값들 개별로 계산하고 그림을 그려야하기 때문에 181개의 값들로 새로운 리스트를 구성해줬습니다
pep = []
for sisi in np.arange(-90, 91, 1):
kk = globals()['ph{}'.format(sisi)]
pep.append(np.array(kk))이 부분은 제가 contour 그림을 그리기 위해서 자료들을 365x181 모양의 형태로 만들어줬습니다
pep 변수는 아직 리스트이기 때문에 아래에서 array로 바꿔주는 작업을 거칩니다
le = np.array(pep)
xx = np.arange(0, 181, 1)
yy = np.arange(0, 365, 1)
X, Y = np.meshgrid(yy, xx)np.meshgrid를 이용해서 2차원 array로 평면 그리드를 만들었습니다
자료를 입력할 좌표점을 만들었다고 생각하시면 됩니다
contour가 등고선이라는 뜻이기 때문에 2차원 좌표를 만들어주고 그 좌표점 위에 값이 올라가면
높이가 생기기 때문에 3차원적인 그래프를 그릴 수 있습니다
plt.figure(figsize = (12, 12))
cs = plt.contour(X, Y, le, 11, cmap = 'inferno')
plt.clabel(cs, inline=True)
plt.xlabel('Julian Day', fontsize = 15)
plt.ylabel('Latitude (\u00b0)', fontsize = 15)
plt.title('Latitudinal Variation of \n Daily TOA Insolation ($Wm^{-2}$',
fontsize = 20, color = 'red')
plt.xticks(np.arange(0, 365, 100), [0, 100, 200, 300], fontsize = 15)
plt.yticks(np.arange(0, 181, 30), [-90, -60, -30, 0, 30, 60, 90], fontsize = 15)여기서 le가 좌표점 위에 올라가는 값들입니다
위도별 일평균 일사량이 되겠죠??
이렇게 실행하고 그림을 보면

이런 그림이 나오게 됩니다
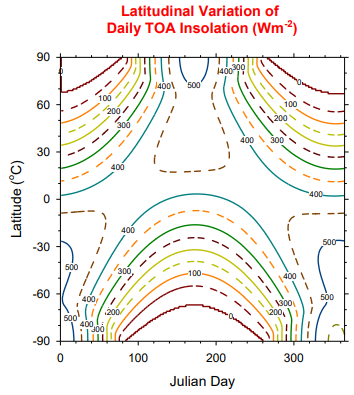
강의노트 그림과 비교해보면 거의 똑같이 그려졌습니다
그림 그리는 툴이 달라서 생기는 차이 정도를 제외하면 거의 비슷한거 같아요
다음은 적도, 북위 30, 60, 90도에서의 그림입니다
fig, ax = plt.subplots(figsize = (9, 5))
ax.plot(mm, ph30, color = 'g', label = 'N30')
ax.plot(mm, ph60, color = 'r', label = 'N60')
ax.plot(mm, ph0, color = 'b', label = 'Eq')
ax.plot(mm, ph90, label = 'N90')
ax.set_xlabel('Julian Day', fontsize = 15)
ax.set_ylabel('Insolation (W/$m^{-2})$', fontsize = 15)
ax.set_title('Changes in solar radiation by latitude \n (0\u00b0N, 30\u00b0N, 60\u00b0N, 90\u00b0N)', fontsize = 15)
ax.set_xticks(tic)
ax.set_xticklabels(['J', 'F', 'M', 'A', 'M', 'J', 'J', 'A', 'S', 'O', 'N', 'D', 'J'])
ax.grid()
ax.legend()이렇게 코드를 만들고 실행해보면

이렇게 그림이 나옵니다
조금 분석을 해보면 적도의 경우 1월부터 상승하고 4월에 최대를 보인 후 오히려 여름에 감소합니다
이는 북반구가 여름이 되면서 북극 부분이 태양에 가장 가까워지게 되고 적도는 상대적으로 살짝
멀어지기 때문에 7,8,9월인 여름에 오히려 하강하는 모습입니다
반대로 북극의 경우 1월 ~ 4월, 10월 ~ 12월까지는 대기 상단 일사량이 아예 없거나 매우 적은 모습입니다
여름으로 갈수록 적도보다도 태양에 가까워지기 때문에 적도보다도 일사량이 많아집니다
가깝고 멀고는 아래 그림을 보시면 이해하실 수 있을거 같아요

마지막으로 위도별 연평균 일사량입니다
fig, ax = plt.subplots(figsize = (4, 9))
ax.plot(gg, ll, color = 'red')
ax.set_yticks(np.arange(-90, 91, 30))
plt.xlim(0, 450)
plt.ylim(-90, 90)
plt.xlabel('Insolation ($Wm^{-2}$)', fontsize = 15)
plt.ylabel('Latitude (\u00b0)', fontsize = 15)
plt.title('Annual Average', fontsize = 20, color = 'red')
ax.grid()이 코드를 실행해보면

이렇게 그림이 나옵니다
아무리 여름에 멀어진다고 해도 적도는 거의 1년 내내 태양에너지를 많이 받기 때문에
적도에서 일사량이 가장많고 양극으로 갈수록 적어지는 모습입니다
이렇게 대기 상단 일사량의 위도 분포를 그려봤습니다
교수님이 과제에 대해 설명을 안해주신 부분들도 있고
코드를 최대한 단순화 시켜보려고 하다보니까 이 과제는 꽤 오래 걸렸던 것 같습니다
다음 포스팅은 NCL이 될 거 같습니다
긴 글 읽어주셔서 감사합니다!!
'파이썬' 카테고리의 다른 글
| 작업29: NCL로 시각화한 자료 파이썬으로 gif 만들기2 (0) | 2023.06.25 |
|---|---|
| 작업28: NCL로 시각화한 자료 파이썬으로 gif 만들기1 (0) | 2023.05.04 |
| 작업26: 파이썬으로 대기 상단 연평균 일사량 계산하고 시각화하기1 (0) | 2023.04.30 |
| 작업17: Python으로 EBM 기후모델 만들기2 (0) | 2023.01.06 |
| 작업16: Python으로 EBM 기후모델 만들기1 (2) | 2023.01.04 |